Rechnen mit Schallpegeln
Schallpegel-Addition
Bei der Einwirkung mehrerer Schallquellen ergibt sich eine Zunahme der Schallimmission. Es dürfen nicht die Pegel in Dezibel, die ja keine physikalischen Größen darstellen, addiert werden. Die Pegel müssen zuerst in physikalische Schalldrücke zurückgeführt werden, aus deren Summe wiederum ein Schallpegel gebildet wird.
Die verschiedenen Schallpegel müssen vielmehr nach folgender Gleichung energetisch addiert werden:
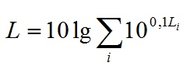
Dazu muss für jeden Summanden Li zunächst der Ausdruck 100,1Li gebildet werden. Hiermit werden die Pegel delogarithmiert, d. h. das Ergebnis stellt das Verhältnis des physikalischen Schalldruckes p zur Bezugsgröße (normierte Hörschwelle) p0 = 2x10-5 Pa dar, welche addiert werden können.
Durch anschließende Logarithmierung der Summe wird wiederum der Pegel aus der Summe der physikalischen Schalldrücke gebildet:
Beispiel:
L1 = 35 dB(A), L2 = 40 dB(A), L3 = 45 dB(A)
L = 10 lg (103,5 + 104,0 + 104,5) = 46,5 dB(A)
Die Pegeladdition lässt sich auch unter Zuhilfenahme der Abbildung 1 jeweils paarweise für zwei Schallpegelwerte ausführen. Dabei liest man mit dem Additionslineal unter der Differenz der zu addierenden Schallpegel (oben) den Wert (unten) heraus, um welchen der größere der beiden Schallpegel im Ergebnis zu erhöhen ist. Hierbei sollten immer zunächst die kleinsten Pegel addiert werden, um die größte Genauigkeit zu erreichen.
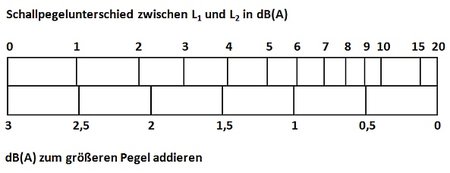
Abbildung 1: Additionslineal
Aus dem Additionslineal der Abbildung 1 kann man die folgende wichtige Regel ableiten:
Unterscheiden sich zwei Schallpegel um mindestens 10 dB, leistet der jeweils niedrigere Pegel zum Summenpegel praktisch keinen Beitrag mehr. Es gilt demnach näherungsweise (mit und ohne Zusatz der A-Bewertung):
65 dB(A) + 54 dB(A) = 65 dB(A)
Die Addition zweier gleicher Schallpegel führt zu einem um drei Dezibel höheren Summenpegel, was einer Verdoppelung der Schalleistung entspricht. Somit gilt z.B.
55 dB(A) + 55 dB(A) = 58 dB(A).
Hinweis:
Viele kleine Pegel können auch zur Pegelerhöhung beitragen trotz Vorhandenseins eines Pegels, welcher mehr als 10 dB höher liegt als diese.
Die Besonderheiten durch die logarithmische Addition zeigt auch Abbildung 2.
Der Schallpegel von zwei gleich lauten Quellen ist nur um 3 dB höher als eine dieser Quellen, obwohl die Schallleistung verdoppelt ist. Der Schallpegel von 10 gleich lauten Quellen ist um 10 dB höher als eine dieser Quellen. Dabei ist die Schallleistung um den Faktor 10 höher als bei einer Quelle.

Abbildung 2: Rechnen mit Schallpegeln
Energetische Mittelwertbildung
Die Mittelwertbildung verläuft analog zur energetischen Schallpegel-Addition, wobei jedoch nach der Addition der Glieder 100,1L durch deren Anzahl zu dividieren ist, und zwar vor dem Logarithmieren.
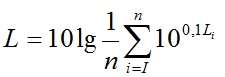
Der Mittelungspegel Lm ergibt sich demnach im Beispiel:
L1 = 35 dB(A), L2 = 40 dB(A), L3 = 45 dB(A) zu
Lm = 10 lg (1/3 (103,5 + 104,0 + 104,5))
Lm = 42 dB(A) (aufgerundet)
Das Beispiel zeigt, dass in einer Reihe unterschiedlicher Schallpegel der energetische Mittelungspegel näher bei den höheren Werten liegt, als es bei einer arithmetischen Mittelwertbildung der Fall wäre.
Da es oft um die Mittelung zeitlich schwankender Geräusche geht, lässt sich die entsprechende Rechenregel dieser Fragestellung dadurch anpassen, dass man statt durch die Anzahl der Werte durch die Gesamt-Beobachtungszeit bzw. Messzeit "T" dividiert und jedes der Additionsglieder 100,1L mit der Einwirkzeit "ti" des Pegelwertes Li während der Gesamt-Messzeit "T" multipliziert.
Wie aus den Regeln der energetischen Pegeladdition und Mittelung leicht abzuleiten ist, gilt im Übrigen:
- Eine Halbierung (Verdoppelung) der Einwirkungszeit eines Geräusches vermindert (erhöht) seinen Mittelungspegel um 3 dB.
- Eine Halbierung (Verdoppelung) der Schallleistung eines Geräusches vermindert (erhöht) seinen Mittelungspegel gleichfalls um 3 dB.
Quelle: Städtebauliche Lärmfibel Online; http://www.staedtebauliche-laermfibel.de/?p=88&p2=2.4.2

